torch 中的 stft、torchaudio 中的 Spectrogram、Melscale、MelSpectrogram 的使用
torch.stft()
1 | |
简介:短时傅里叶变换
其中:
- input(Tensor) 代表输入信号
- n_fft(int) 代表快速傅里叶变换的序列长度
- hop_length(int) 代表相邻两个滑动窗口帧之间的距离,也即是帧移
- win_length(int) 代表窗口大小,默认等于 n_fft
- window(Tensor) 代表窗口函数,默认是矩形窗口(全1)
- center(bool) 代表是否对输入tensor在两端进行padding,使得第 $t$ 帧是以 $t \times hop_length$ 为中心的,默认为 True,如果为 False,则第 $t$ 帧以 $t \times hop_length$ 开始。
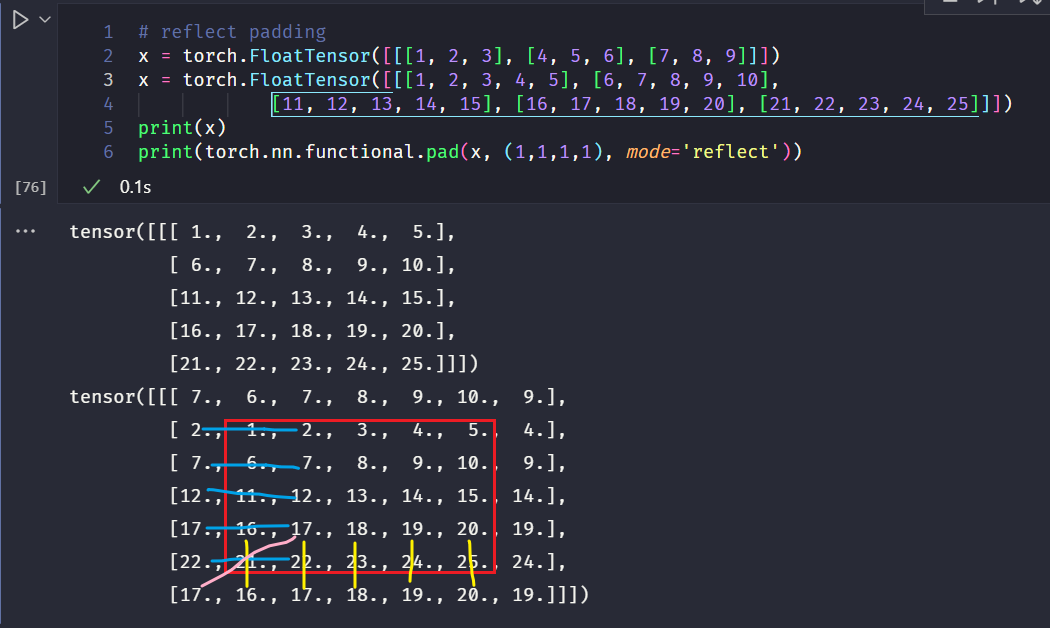
- pad_mode(str) 代表padding的模式(当center为True才有效),默认为 reflect,即对边界的值进行reflect padding
- normalized(bool) 代表是否对返回的STFT结果进行归一化,默认为 False
- onesided(bool) 代表是否只返回一侧的STFT结果(当输入Tensor为实数时,输出为对称的),当输入Tensor和window都为实数时默认为 True,反之为 False
- return_complex(bool) 代表返回实部和虚部的STFT结果还是返回复数
输出:
- output(Tensor) 代表输出的STFT结果,维度为 $\star \times N \times T$,$\star$ 代表 batch size,$N$ 代表频率域的维度,$T$ 代表时间域的维度。
计算表达式为:
$$
X[\omega, m] = \sum_{k=0}^{\text {win_length-1 }} \text { window }[k] \text { input }[m \times \text { hop_length }+k] \exp \left(-j \frac{2 \pi \cdot \omega k}{\text { win_length }}\right)
$$
其中,$m$ 为滑动窗口的索引,$\omega$ 代表频率,当 onesided=False 时,$\omega$ 的取值范围为:$[0, \text { n_fft }]$,当 onesided=True 时,$\omega$ 的取值范围为:$[0, \lfloor \frac{\text { n_fft} }2 \rfloor ]$
注意:上面的表达式是加窗的短时傅里叶变换,但是在计算过程中,往往采用快速傅里叶变换来计算每个 $m$ 对应的帧,因此 n_fft 和 win_length 可以不相等,计算时对加窗后的信号进行补零到 n_fft 的长度,所以需要满足: 0 < win_length <= n_fft
当参数center默认为True时,此时会对信号进行padding,第 $0$ 帧以 $x[0]$ 居中,且左右两边 padding 的长度为 $\lfloor \frac{\text { n_fft} }2 \rfloor$,输出的帧数为 $T = \lfloor \frac{\text{seq_len}}{\text{hop_length}}\rfloor + 1$ 其中,seq_len 代表输入tensor的序列长度。
而当设置center参数为False时,第 $0$ 帧以 $x[0]$ 为开头,输出维度很奇怪??
在频域维度,当
oneside=True输出的 $N = \frac{\text { n_fft} }2 + 1 $ ,当oneside=False输出的 $N = \text { n_fft}$
最后,由于此时并不知道输入信号的采样频率, 所以输出的频率没有具体值。或者说,输出矩阵在频率轴的值对应的频率为 $\omega = \frac{2\pi}{N}k$,其中,$k$ 为频率轴的索引,且这里的 $\omega$ 为DSP中常说的数字角频率,他和模拟频率 $f$ 的关系为:$\omega = \frac{2\pi f}{f_s}$,其中 $f_s$ 为输入信号的采样频率,那么 $k=\frac{\text{n_fft}}{2}$ 为频率轴信号的最高频率(假定
oneside=True),对应的具体值为采样率的 $1/2$,而这也符合奈奎斯特采样定理:为了不失真地恢复原始信号,采样率必须大于测量信号最大频率的两倍 $f_s > 2 \times f_N$
torchaudio.transforms.Spectrogram
1 | |
简介:求输入信号的语谱图
其中:
- n_fft 为FFT的长度,默认为400,会生成 n_fft // 2 + 1 个 bins
- win_length 为窗口的长度,默认为 n_fft
- hop_length 为相邻两个滑动窗口帧之间的距离,即帧移,默认为 win_length // 2
- pad 为对输入信号两边的补零长度,默认为 0
- window_fn 为窗函数,默认为 torch.hann_window
- power 为语谱图的幂指数,默认为 2.0,值必须大于 0,取 1 代表能量,取 2 代表功率。
- normalized 为是否对语谱图进行归一化,默认为 False
- wkwargs 为窗函数的参数,默认为 None
- center 为是否对输入tensor在两端进行padding,使得第 $t$ 帧是以 $t \times hop_length$ 为中心的,默认为 True,如果为 False,则第 $t$ 帧以 $t \times hop_length$ 开始。
- pad_mode 为补零方式,默认为 reflect
- onesided 为是否只计算一侧的语谱图,默认为 True,即返回单侧的语谱图,如果为 False,则返回全部的语谱图。
- return_complex 不再使用了
求解Spectrogram的本质其实还是stft,因此当
power=1时,输出的就是stft的能量谱。当power=None时,就是直接输出了stft的结果,当power=2时,输出就是power=1的值的平方。
torchaudio.transforms.MelScale
1 | |
简介:用来将stft的结果转换为mel域中的stft的结果。
其中:
- n_mels(int) 为mel滤波器的个数,默认为128
- sample_rate(int) 为音频采样率,默认为16000
- f_min(float) 为音频的最小频率,默认为0.0
- f_max(float) 为音频的最大频率,默认为采样率二分之一: sample_rate // 2
- n_stft(int) 为stft的bin的个数,不给的话默认为None,从第一个输入计算得到。
- norm(str) 如果为“slaney”,则将三角形mel权重除以mel bin的宽度(即进行面积归一化),默认为None
- mel_scale(str) 采用的mel尺度: htk 或者 slaney,默认 htk
输入:
- input(Tensor) Spectrogram 的输出,其维度为 $\star \times n_stft \times T$
输出: - output(Tensor) 返回大小为 $\star \times n_mels \times T$ 的Tensor
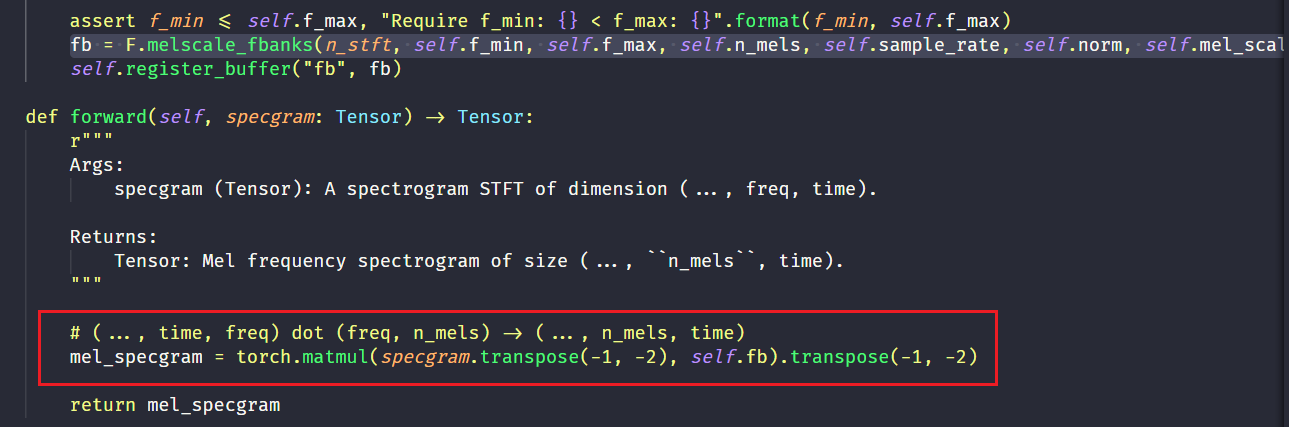
这一过程其实就是首先计算一个 $\star \times n_stft \times n_mels$ 的滤波器组矩阵,这个矩阵体现了信号频率 和 mel 域频率之间的转换关系,然后和输入的 Spectrogram 做矩阵乘法:
最后求得mel域的Spectrogram,即Mel谱。
注意:计算Spectrogram的时候不需要采样率,这是因为输出的频率是数字域角频率,而在计算MelScale的时候,需要具体的模拟频率和Mel域频率之间的转换关系,因此需要采样率来求出模拟频率的具体值,最后再转换到Mel域频率。
torchaudio.transforms.MelSpectrogram
1 | |
简介:求输入信号的Mel谱
其中:
- sample_rate(int) 为输入波形的采样率
- n_fft(int) 为FFT的长度,默认为400,会生成 n_fft // 2 + 1 个 bins
- win_length 为窗口的长度,默认为 n_fft
- hop_length 为相邻两个滑动窗口帧之间的距离,即帧移,默认为 win_length // 2
- f_min(float) 为音频的最小频率,默认为0.0
- f_max(float) 为音频的最大频率,默认为None
- pad 为对输入信号两边的补零长度,默认为 0
- n_mels(int) 为mel滤波器的个数,默认为128
- window_fn 为窗函数,默认为 torch.hann_window
- power(float) 为语谱图的幂指数,默认为 2.0,值必须大于 0,取 1 代表能量,取 2 代表功率。
- normalized(bool) 为是否对stft的输出进行归一化,默认为 False
- wkwargs 为窗函数的参数,默认为 None
- center(bool) 为是否对输入tensor在两端进行padding,使得第 $t$ 帧是以 $t \times hop_length$ 为中心的,默认为 True,如果为 False,则第 $t$ 帧以 $t \times hop_length$ 开始。
- pad_mode(str) 为补零方式,默认为 reflect
- onesided(bool) 为是否只计算一侧的谱图,默认为 True,即返回单侧的语谱图,如果为 False,则返回全部的谱图。
- norm(str) 如果为“slaney”,则将三角形mel权重除以mel bin的宽度(即进行面积归一化),默认为None
- mel_scale(str) 采用的mel尺度: htk 或者 slaney,默认 htk
输入:
- input(Tensor) 输入波形信号
输出:
- output(Tensor) 输出Mel谱
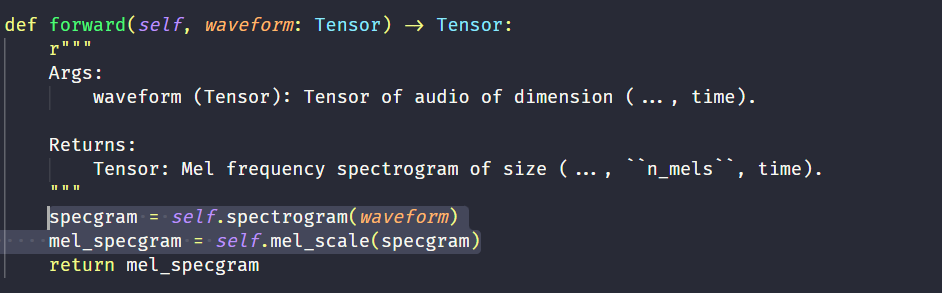
可以看出,MelSpectrogram的参数完全就是Spectrogram的参数+MelScale的参数。实际上,这个函数的计算过程就是在里面先计算spectrogram再计算mel_scale:
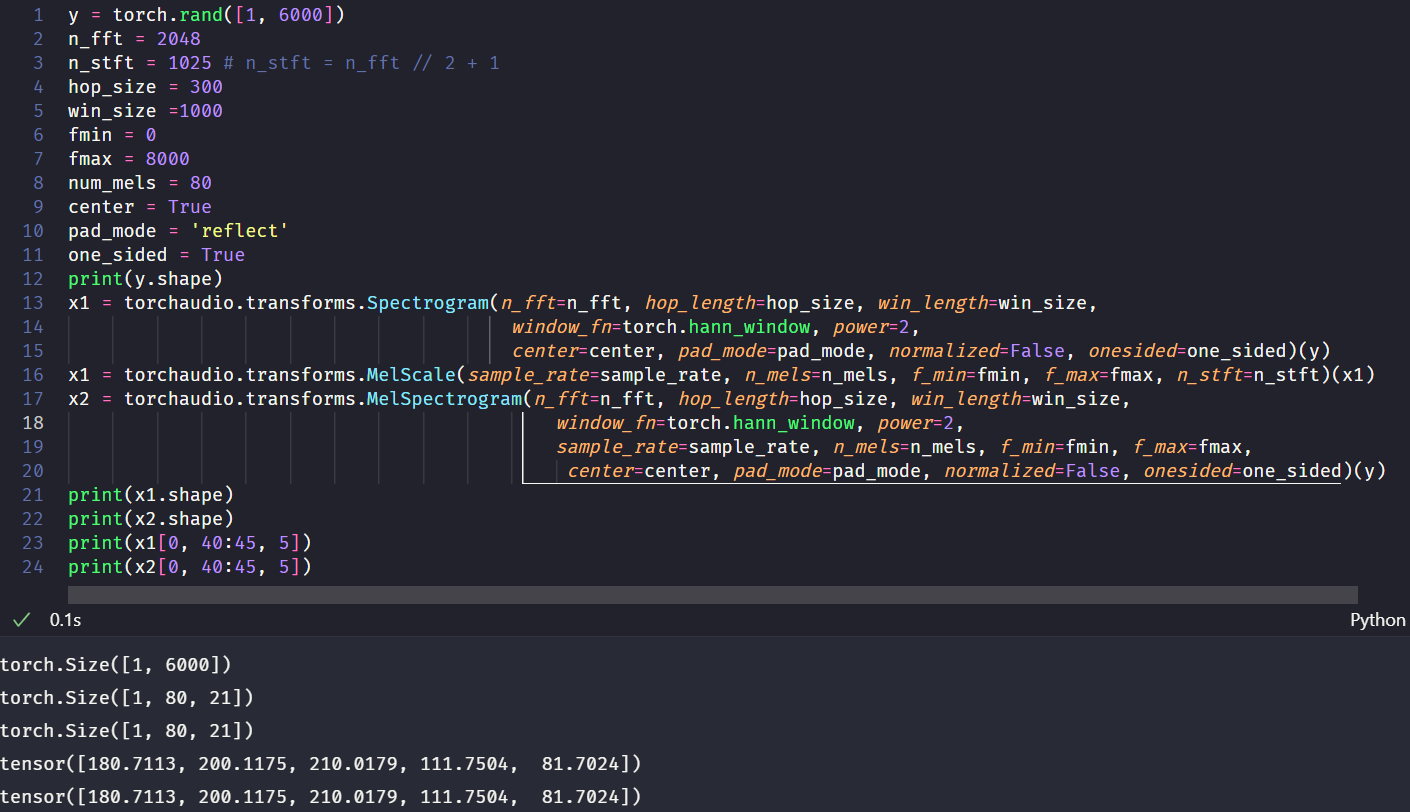
测试结果也验证了这一点:
用两种方法计算的mel谱结果完全一样。
其他
- 关于信号的能量谱和功率谱(参考):
- 能量谱:通常用来描述能量信号(能量有限的信号称为能量信号),表示的是信号在各个频点中的能量分布情况,如果对能量谱在频域进行积分,则可以求出信号的总能量。
- 功率谱:通常用来描述功率信号(功率有限的信号称为功率信号),是指用密度的概念表示信号功率在各频率点的分布情况,对功率谱在频域上积分就可以得到信号的功率。
- 维纳-辛钦定理:信号的功率谱和其自相关函数是一对傅里叶变换。在工程实际中,即便是功率信号,由于持续的时间有限,可以直接对信号进行傅里叶变换,然后对得到的幅度谱的模求平方,再除以持续时间来估计信号的功率谱。
- 根据上面的解释,
torchaudio.transforms.Spectrogram求功率谱时并没有除以持续时间,而是直接输出了平方值。
- 关于Spectrogram和stft:
- 当
torchaudio.transforms.Spectrogram网络中的power=1时,输出的Spectrogram是能量图,在其他参数完全相同的情况下,其输出结果和torch.stft函数中return_complex=True的输出再求复数的模值之后的结果相同: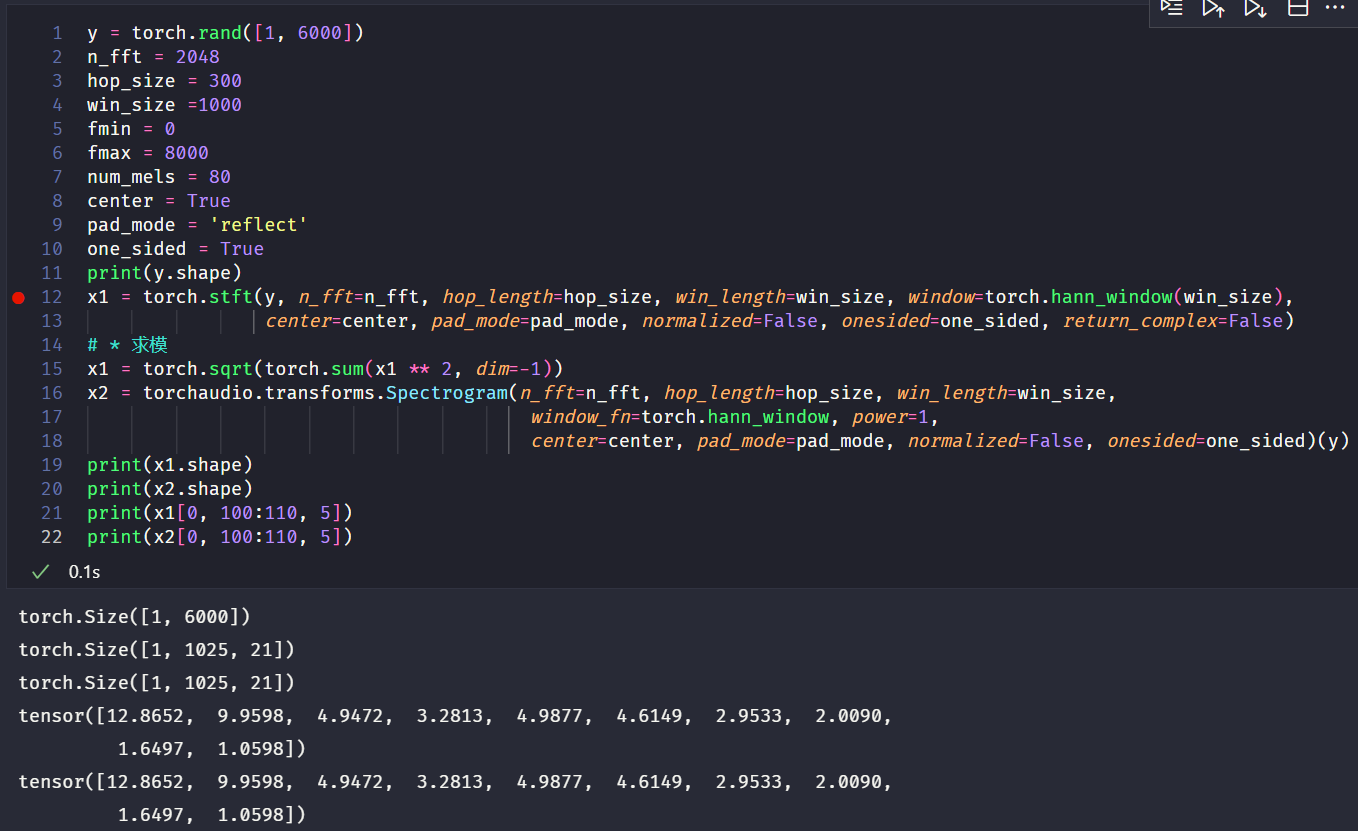
图中,$x_1$ 是stft函数求模之后的结果,$x_2$ 是直接求Spectrogram得到的结果。 - 当
torchaudio.transforms.Spectrogram网络中的power=None时,输出的Spectrogram是sftf的直接结果,在其他参数完全相同的情况下,其输出结果和torch.stft函数中return_complex=True完全相同: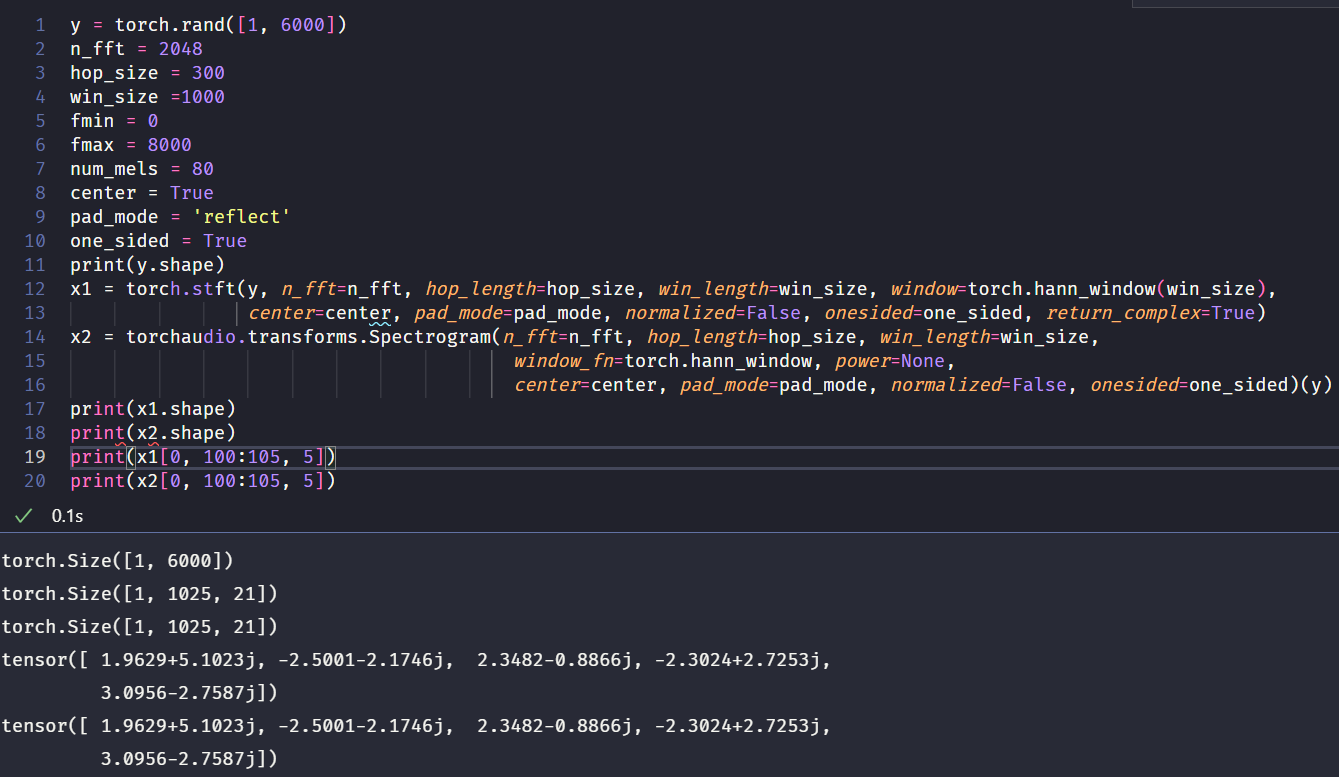
图中,$x_1$ 是stft函数之后的结果,$x_2$ 是直接求Spectrogram得到的结果。 - 事实上,Spectrogram内部就是调用了stft的计算:
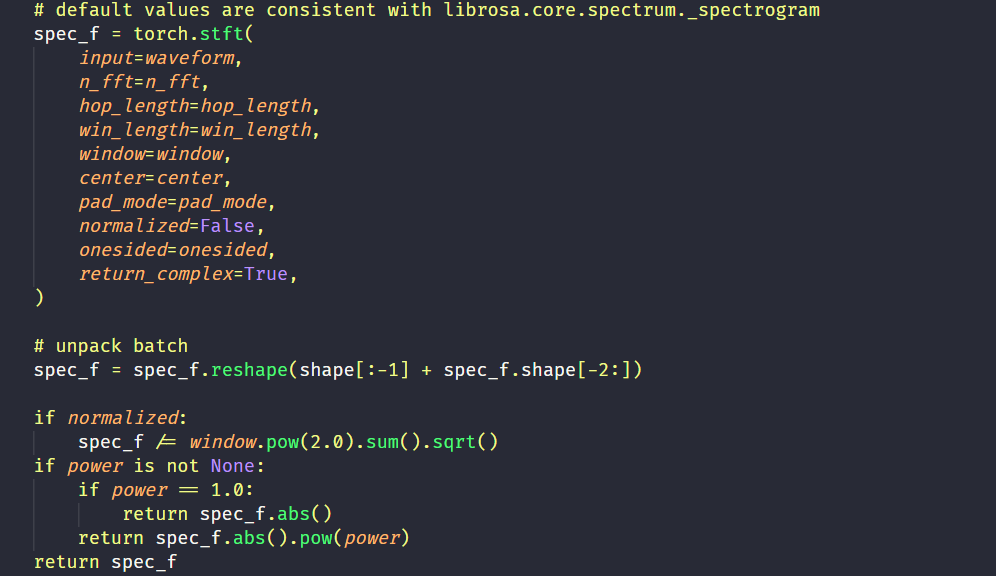
然后根据power取值计算最终的输出。
- reflect padding : 以矩阵的边界为对称轴,将内部的数据复制到外部: